يتألّف السَّمَد الخالِمي أو الاستطالي من خطّي أعداد متعامدين، يُسمّى كلّ منهما محورا، ويتقاطعان في نقطة تُسمّى الرَّسّ والرَّسِيس origine، يُسمّى المحور الأفقي بالساف abscisse وهو المحور السيني، ويُسمّى المحور العَمَدي بالزاف ordonnée وهو المحور العيني، كلّ نقطة «أ» في خالِم المحاور التآلفية، يمثّلها زوج مرتّب من المَسامِد (س، ع)، حيث يُسمّى «س» بالمَسْمد السافي، ويُسمّى «ع» بالمسمد الزافي للنقطة «أ».

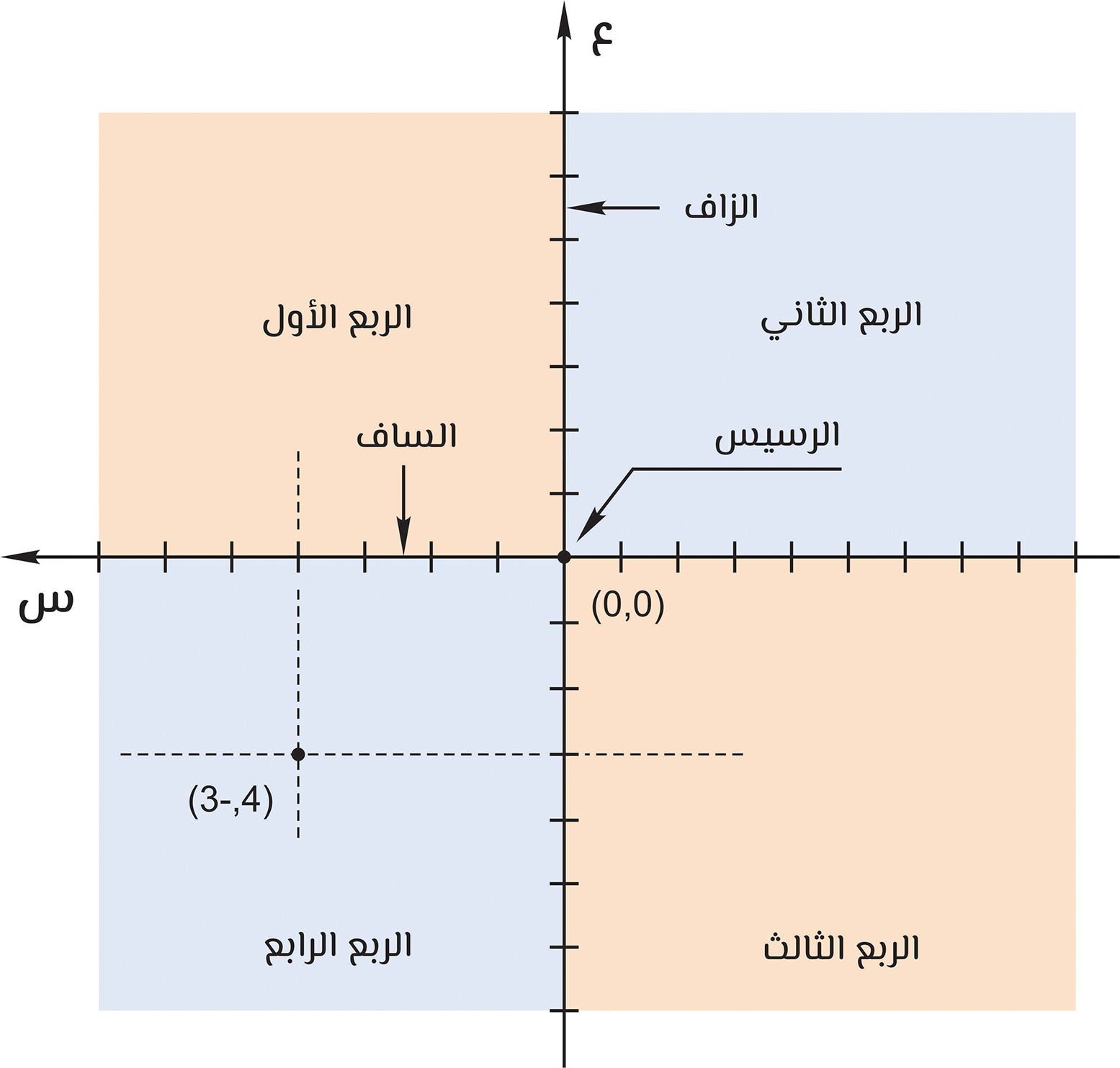
نظام السَّمَد الاستطالي

يُقسّم الخالِم الاستطالي إلى أربعة أقسام، يُسمّى كلّ قسم منه بالرُّبع، الربع الأوّل يتكوّن من أزواج مرتّبة، تكون مسامدها موجبة، الربع الثاني يتكوّن من أزواج مرتّبة تكون مسامدها الأولى سالبة ومسامدها الثانية موجبة، والربع الثالث يتكوّن من أزواج مرتّبة تكون مسامدها سالبة، ويتكوّن الربع الرابع الأخير من أزواج مرتّبة، تكون مسامدها الأولى موجبة، والثانية سالبة، لرسم النقطة (4، -3) نتحرّك أربع وحدات في الاتجاه الموجب على الساف وهو المحور السيني، وثلاث وحدات في الاتجاه السالب على الزاف وهو المحور العيني، وعند التقاطع تكون النقطة (4، -3).

تصف المسامِد الخالِمية موضع نقطة على خَالِم باستعمال زوج من الأرقام التي تبيّن كيفية الوصول إلى هذه النطقة من رسيس محدّد، قدّمها الفيلسوف والتياسي الفرنسي «رينيه ديكارت» في القرن التاسع عشر الميلادي، وهي تعمل مثل أنظمة المسامِد المستعملة على الخرائط وتسهل التعيين الهندسي للأشياء. ويتمّ تعيين هذه النقطة على نحو ما يُستعمل في المسامد الإراضية. في خالِم ثنائي البعد، تتميّز نقطة ما بمَسْمدين (س، ع) ممّا يعني أنّه يجب الانتقال بمقدار «س» وحدات في الاتجاه الأفقي، ثمّ الانتقال بمقدار «ع» وحدات في الاتجاه العَمَدي، أمّا النقاط السالبة (-1، -2) فتدلّ على أنّ الانتقال يكون في الاتجاه المعاكس، كما أنّ مَسْمدي الرسيس هما (0,0).

السَّمَد من السَّمْد وهو القصد، يُقال سَمده بمعنى قصده واعتمده، والمَسْمَد المقصد. الزاف من الزَّيْف وهو الارتفاع، وقد زاف البناءُ زَيْفًا: طال وارتفع. والساف أصل البناء الذي يقوم عليه الجدار، والرَّسّ والرسيس مبتدأ كلّ شيء. الخالِم plan هو المعروف بالمُسْتوي، تُجمع هذه الكلمة على خَوالم وأصلها في اللغة المستوي الذي لا يفوت بعضه بعضا. كلمة abscisse الفرنسية أصلها في العربية أسِيس، فالأسّ والأسيس من كلّ شيء أصله، وكذلك أصل البناء، فالحرف «b» مُلتّب أي مزيد زيادة قياسية، فصيغتها الأصلية هي ascisse، أمّا ordonnée فأصلها عرض ord-onnée أي ord، فالحرف «o» يُبدل من عين، مثل odeur بمعنى عُطور. الكاسعة (onnée) تنوين الرفع في العربية.