اعتمدت تجارب «لينوس بولينغ» Linus Pauling سنة 1929م لتحديد قواعد التناسق في المعادن على دراسة البلورات الشاردية، ولما كانت بعض الروابط من الصنف التساهمي أو التكافؤي، فقد صنع ذلك مشكلة إلى حدّ ما، وعلى الرغم من ذلك فإنّ هذه القواعد يمكن تطبيقها على أغلب المعادن. وتتلخّص أساسا في مُنصَّل التناسق، وارتباط المُنصَّلات بعضها ببعض، وقاعدة الشِّحّة.

مُنصَّل التناسق

في أي نوع معدني معيّن تتجمّع الحواصر على شكل هندسي ثابت حول الشوابر، فالهيكل البلّوري الذي يُبنى من هذا التجمّع يُسمّى مُنصَّل التناسق polyèdre de coordination حيث تحتلّ الحواصر قُرَن أو قِمم هذا المُنصَّل بينما تندسّ الشوابر داخل الفراغات التي تنشأ من هذا الهيكل البلّوري المتراصّ. أكثر المعادن ولا سيّما الكَوْثبات لها روابط في الكثير الغالب شاردية، ويمكن تمثيل تركيبها على شكل تجمّعات من الكرات المتراصّة حيث تكون الشوابر محاطة بالحواصر، وممّا هو معلوم فإنّ عدد الحواصر يتحدّد بحجم الشابرة، فكلّما كانت الشابرة كبيرة كان عدد الحواصر المحيطة بها كبيرا أيضا. يُعتبر الكثار العنصر الأكثر وفرة في القشرة الأرضية حيث يكوّن أزيد من 90% من حجمها، لذلك نقوم بتحديد نَساقة شاردة ما من خلال نسبتها إلى الكثار، كما يمكن أيضا تحديدها من خلال ذرّات الهُبان، أو الكبريت، أوّ أي ذرّة قريبة منها، فالحواصر عادة ما تكون كبيرة الحجم مقارنة بالشوابر، لذلك تصنع الحواصر هيكلا بلّوريا على شكل هندسي وتتوضّع الشابرة داخل هذا الهيكل.

عندما تتجمّع الشوارد الكروية مع بعضها بعضا وتنتظم، فإنّ استقرارها يكون أكبر ما يمكن عندما تكون الشوارد متلامسة بجوار بعضها بعضا، وتنتظم بشكل متناظر، وتتحدّد البِنية البلّورية الشاردية بعاملين، الأوّل حجوم الشوارد، والثاني التعادل الكهربي الكلّي للبِنية. للحجم أهمّية كبيرة في تحديد الشكل الهندسي للهيكل كما أنّ له علاقة مباشرة بالنساقة أو العدد التناسقي أو التساندي coordinence فهو عدد الشوارد السالبة التي تكون الأقرب إلى الشابرة والتي تحيط بها، فالهياكل التي يصنعها هذا الترابط بين الذرّات تكون على شكل:

- مثّلث : حيث يكون مركز كلّ الحواصر التي تحيط بالشابرة في خالِم واحد، ويُساوي عدد التناسق في هذه الحال 3، مثال ذلك: س⁴⁺، ع⁵⁺، سا³⁺.

- رِكات : يكون مركز ثلاث ذرّات من الحواصر في خالم واحد، ويكون مركز الحاصرة الرابعة خارج هذا الخالم. يصل العدد التناسقي في هذا التركيب إلى 4، مثال ذلك: هف³⁺، كا⁴⁺، هـ⁶⁺.

- دِكات : يتوضّع مركز أربع حواصر في خالم واحد، وتكون حاصرة واحدة في كلّ جنب من الجنبين. يصل العدد التناسقي في هذا التركيب إلى 6، مثال ذلك: ل²⁺، ح²⁺.

- كَعْب : يصل العدد التناسقي في هذا التركيب إلى 8، مثال ذلك : قل⁺، سن^-.

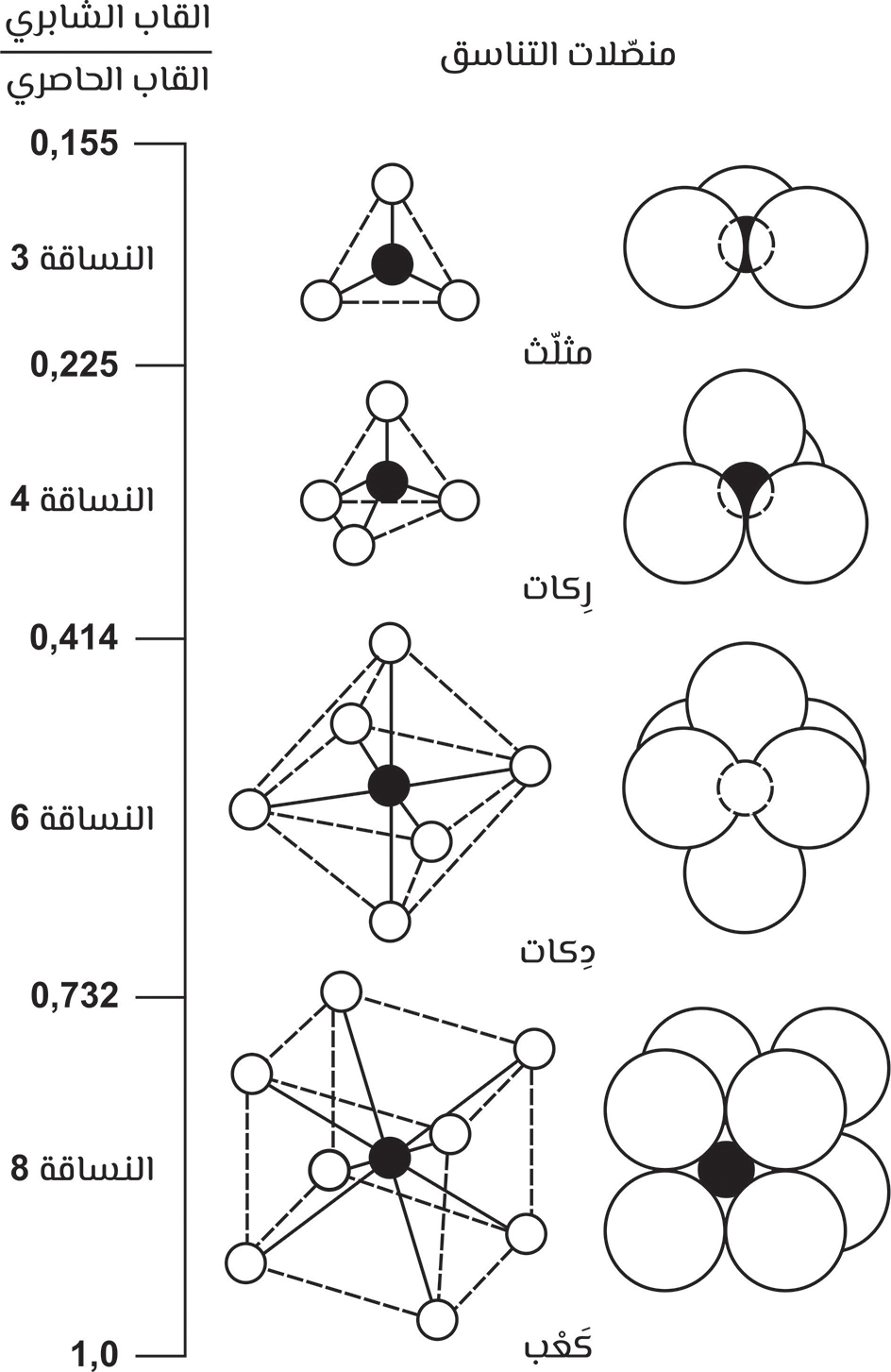
جدول يُبيّن العلاقة بين نسب الأقواب الشاردية والنساقة

في مُنصَّل التناسق تُعتبر المسافة الأقصر التي تفصل بين نواتي حاصرة وشابرة هي مجموع قيمتي القاب الشاردي لكلّ منهما، مع اعتبار أنّ الشوارد ما هي إلاّ كُرات صلبة ومتماسّة بجوار بعضها بعضا، ويبلغ أقصى عددها التناسقي 12 وذلك عندما تنتظم الكرات المتساوية في المقياس وَفْق قانون المنظومات المتراصّة، كما يوجد أيضا العدد التناسقي 5 على شكل هرم رباعي في مجموعة (بس₂ك₈)^8-، أمّا العدد التناسقي 7 و9 فنادر الوجود، ويكون حول شوارد مثل: ص²⁺، شر²⁺، بر³⁺، الخ. إنّ تسمية الرِّكات والدِّكات، الخ، لا يعني أبدا أنّ المنصَّلات منتظمة بشكل مثالي، فتناظرها يعتمد على عناصر التناظر التي تمرّ عبر موقع الذرّة المركزية، وسيكون هذا المُنصّل مشوّها إلى حدّ ما حسب الحالات، فالروابط بين الفلزّات والكُثار تُحدِث اختلافا ملحوظا في الطول. وتعتبر دراسة تناظر مواقع الشوارد ذات أهمّية كبيرة لتفسير أطياف امتصاص الأشعة تحت الحمراء على سبيل المثال، ثمّ إنّ دِكات التناسق يكتسب تناظرا مختلفا حسب كلّ معدن معيّن.

ارتباط المنصَّلات

لا ترتبط مُنصَّلات التناسق فيما بينها بواسطة أنصلتها أبدا، لأنّه في حال ما تشارك مُنصَّلان في نصيل واحد، فستكون المسافة بين شابرة وشابرة قريبة جدّا مقارنة بالمسافة بين الشابرة والحواصر في المُنصَّل نفسه، وسيكون التنافر بينهما كبيرا يفوق قوّة الجذب بين الشابرة والحواصر التي تحيط بها، وهذه هي الحالة العامّة الموجودة في الطبيعة، فأركتة التناسق لذرّة الكثاب، لا ترتبط فيما بينها عن طريق الأنصلة، بل يكون الارتباط بين المنصّلات بواسطة القُرن، وفي القليل النادر ما يكون بالأضلع.

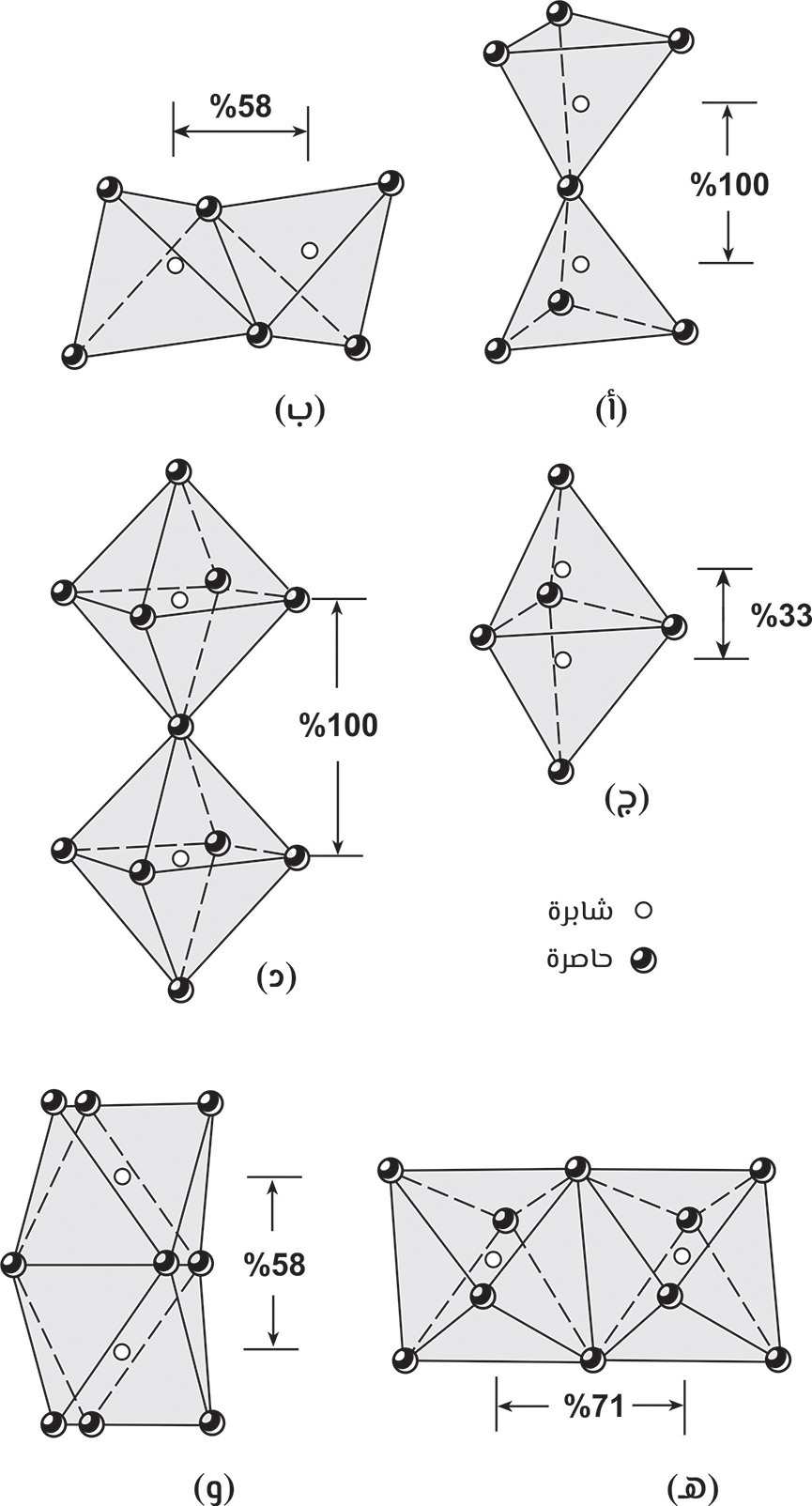
في بِنية مستقرّة فإنّ الأركتة تتقاسم القُرَن (أ)، وليس الأضلع (ب) أو الأنصلة (ج)، لأنّ هذا من شأنه أن يجعل الشوابر قريبة جدّا من بعضها بعضا. بالنسبة للأركتة في (د)، و(هـ)، و(و)، فإن المسافات بين الشابرة والشابرة كبيرة إلى حدّ يمكن للبنية البلورية أن تنشأ أيضا على هذا الوضع.

التساوي في عدد التكافؤ الكهسني

تنصّ هذه القاعدة على أنّ مجموع التكافؤات الكَهْسَنِية للشوابر في بلّورة شاردية مستقرّة، يجب أن يتساوى مع عدد تكافؤ الحاصرة التي تحيط بها هذه الشوابر، وذلك لضمان التعادل الكهربي الموضعي للبلّورة. وبعبارة أخرى، في البنية البلّورية المستقرّة، تكون الروابط الكلّية التكافؤية التي تصل إلى الحاصِرة من جميع الشوابر المجاورة لها مساوية لشحنة الحاصرة. يحتاج هذا إلى شرح أعمق، يمكن تعريف الرابطة الكهسنية (الإلكتروستاتيكية) (تك) بأنّها شحنة التكافؤ الشاردي (ش) مقسومة على العدد التناسقي (ن)، حيث تك= ش\ن معبّر عنها بالقيم المطلقة أي من دون إشارة لعلامة زائد أو ناقص، العدد الناتج يُسمّى التكافؤ الكهسني electrostatic valency (تك) وهو مقياس لقوّة أي من الروابط التي تصل إلى شاردة التناسق من أقرب جيرانها، على سبيل المثال، في العسجر ق.سن، تحيط ستّ حواصر من سن- شابرة واحدة من القلان ق+ في نساقة دِكاتية، وتصل إلى ق+ من كلّ رابطة تحيط بها قوّة (تك) مقدارها 1\6، ويعني هذا أن هناك ستّ روابط تحيط بالقلان المركزي من ستّ ذرّات مجاورة لها (سن-) تقوم تماما بتحييد شحنة القلان المركزي بشكل كامل، وكذلك بالنسبة للشاردة سن- لها أيضا ستّ ذرات مجاورة لها من القلان ق+، وتصلها من كلّ ذرّة قلان رابطة بقوّة 1\6، ويقوم مجموع هذه الروابط بتحييد الشحنة على سن-.

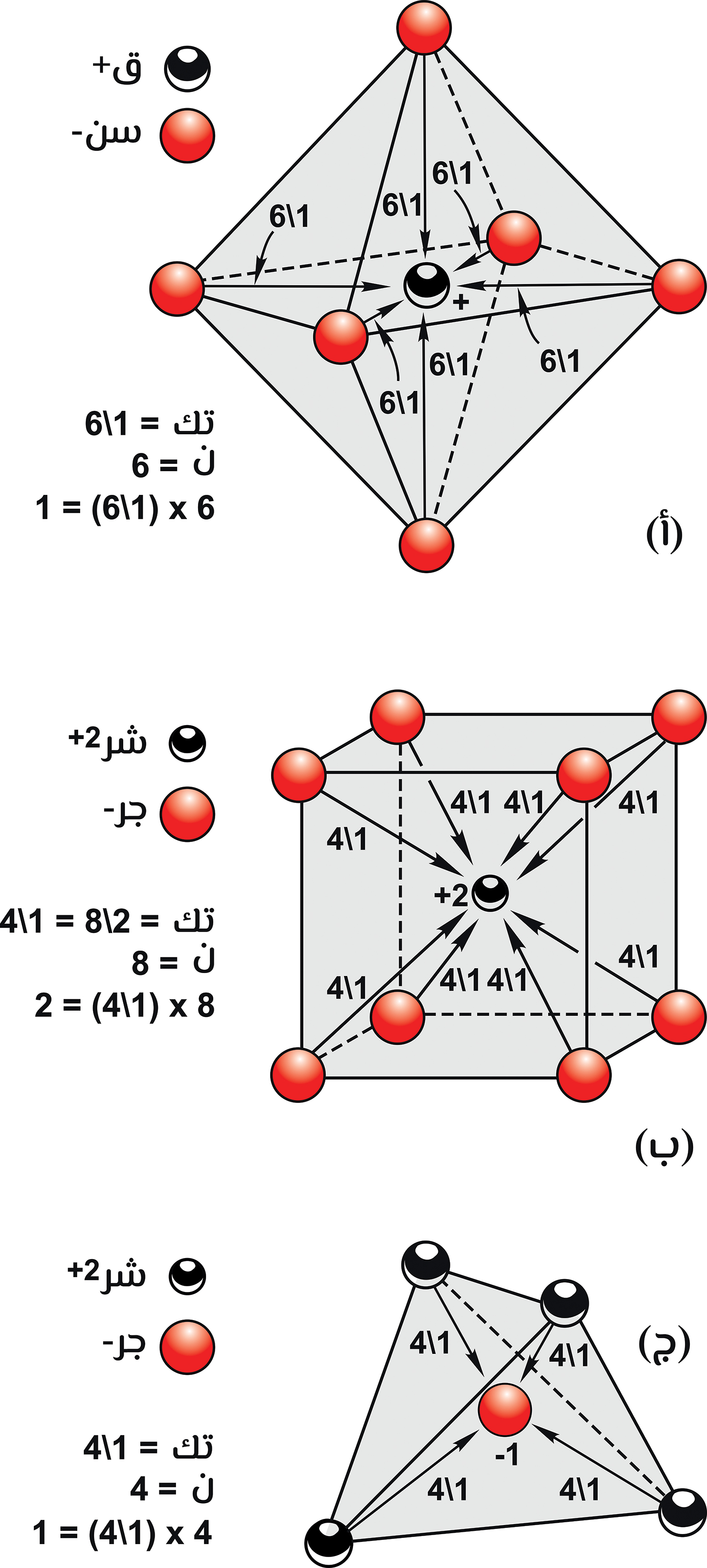
تنجيل يبيّن تحييد شاردة مركزية بالروابط المحيطة بها، ولكل من هذه الروابط تكافؤ كهسني (تك). مجموع كلّ الروابط يحيّد الشاردة المركزية. (أ) نساقة دِكاتية في العسجر. (ب) نساقة مكعبة للدجار حول الشراق في بِنية الخُشاش. (ج) نساقة رِكاتية للشراق حول الدُّجار في بِنية الخُشاش.

تقدّم هذه الأشكال أمثلة عن التكافؤ الكهسني في منصّلات تناسق إضافية. إنّ قاعدة التكافؤ الكهسني مفيدة جدّا في تقييم الطبيعة المُنصّلية للهياكل البلّورية. في بِنية مستقرّة، فإنّ مجموع التكافؤات الكهسنية للشوابر في منصّلات التناسق، يُوازِن بالضبط الشحنة على الحاصرة التي تتقاسمها منصّلات التناسق، على سبيل المثال في البنية البلّورية للبنفش الشَّدَهاني grossular garnet (شر₃هف₂كا₃ك₁₂)، يكون شر²⁺ في نساقة مكعبة (العدد التناسقي ن=8)، هف³⁺ في نساقة دِكاتية (ن=6)، وكا⁴⁺ في نساقة رِكاتية (ن=4) وكلّ هذه الذرّات تحيط بالكُثار، وروابطها لها تكافؤات كهسنية على التوالي: 2\8= 1\4، 2\6= 1\3، 4\4= 1، وأخير فمن أجل تحييد شحنة مقدارها 2 على الكُثار المشترك، فإنّ شاردة الكثار هذه يجب أن تنتمي إلى مُنصّلين مكعّبين شر²⁺، ودِكات واحد هف³⁺، ورِكات واحد كا⁴⁺ (2*1\4+ 1\2+ 1= 2)، وهذا هو الرابط الأساسي لمنصّلات التناسق linkage of coordination polyhedra في البنفش. مثال آخر: للبُهار أو الدهاش topaze الصيغة الكيميائية: هف₂كاك₄(جر،ك.ها)₂ وفيه تكون شاردة الكثار مُحاطة بذرة كُثاب واحدة وذرّتي زُهاف: فمجموع التكافؤات الكَهْسَنِية (نسبة التكافؤ للعدد التناسقي) هو: 4\4+ 2(3\6)= 2، وهو عدد التكافؤ الكيميائي لذرّة الكُثار.

هناك قاعدة أخرى ذكرها بولينغ وتنصّ على أنّه في بلورة تحتوي على شوابر مختلفة، فإنّ تلك التي تشتمل على التكافؤ العالي والنساقة الصغيرة تميل إلى ترك تقاسم العناصر المنصّلية فيما بينها وهي القُرَن والأضلع والأنصلة، وفي حال ما تقاسمت هذه العناصر وتشاركتها فإنّ الأضلع المشتركة تتقلّص لوضع المزيد من الشحنات السالبية بين الشوابر، وتُزاح الشوابر عن مراكزها في المنصّلات، بعيدا عن الضلع المشترك أو النصيل لتقليل التنافر بين الشابرة والشابرة. وقد صمّمت كلّ القواعد التي ذكرت آنفا على أساس واحد وهو، زيادة عوامل الجذب الشابري-الحاصري إلى أقصى حدّ وتقليل التنافر بين الحواصر والتنافر بين الشوابر.

قاعدة الشِحّة

تنصّ قاعدة الشِّحّة principle of parsimony على أنّ عدد الشوارد ذات الطبيعة المختلفة والتي تدخل في بناء مُنصّل التناسق، يكون قليلا جدّا، نجد مثال ذلك في شاردة الكُثاب 4+، حيث لا تحيط بها إلاّ ذرّات الكُثار وهي أربع ذرّات، كما يُلاحظ أيضا أنّ العائلة الضخمة للكوثبات لم تؤسَّس إلاّ على عشرات من العناصر الكيميائية، فلا يمكن أن يحتوي نوع معدني ما في المتوسّط أكثر من 5 إلى 6 عناصر.

الكَهْسنة مصطلح منحوت من كهربة وساكنة، والرِّكات هو ما يُعرف برباعي الوجوه، وقد سُمّي بحروف العدد، ومثله الدِّكات ومعناه ثُماني الوجوه، المُنصّل هو كثير الأنصلة المعروف بكثير الوجوه، فالنصيل وجه البلوّرة والمعدن والحجر. أمّا الكَعْب فهو الاسم لما يُعرف بالمكعّب، وسُمّيت الكعبة المشرّفة كعبةً لتربّع أركانها. أمّا المُكعّب فهو صفة، ومثله المستوى أو المستوي، حيث يُستعمل للدلالة على ثلاثة معانٍ، الأوّل هو درجة العلو بالنسبة لسطح مستو ويُقابل كلمة niveau في الفرنسية، والمعنى الثاني هو السطح المستوي الذي له بُعدان فقط، ويقابل كلمة plan في الفرنسية، المعنى الأخير هو الصفة لما كان مسطّحا مستو في تسطيحه، ولتقليل الاشتراك اللفظي اُستعمل مصطلح الخالِم plan للدلالة على الشكل الهندسي ببعدين، ومعناه اللغوي المستوي الذي لا يفوت بعضه بعضا، الجمْع خوالم، ومثل هذا أيضا المستطيل والمربع والمثلّث والمُعيّن كلّها مصطلحات غير موفّقة، ومن الحزم نَبْذها واصطناع مصطلحات أخرى بدلا عنها تكون أسماء وليست صفاتا. أصل كلمة niveau الفرنسية هي في اللغة العربية «نَحْو» بمعنى المثل والمقدار، فالحرف «v» يُبدل من حاء، والكاسعة eau أصلها الواو المجزومة.